数据结构
链表
链表的基础实现
判断链表是否有环及环入口索引
代码测试
时间复杂度分析
代码文件如下:
链表的基础实现
class Node:
def __init__(self, data):
self.data = data
self.next = None
class LinkList:
def __init__(self):
self.head = None
def isEmpty(self):
return self.head is None
def length(self):
cur = self.head
count = 0
while cur is not None:
count += 1
cur = cur.next
return count
def add(self, data):
# 在头部插入元素
new_node = Node(data)
if self.head is None:
self.head = new_node
else:
new_node.next = self.head
self.head = new_node
def append(self,data):
new_node = Node(data)
if self.head is None:
self.head = new_node
else:
cur = self.head
while cur.next is not None:
cur = cur.next
cur.next = new_node
def insert(self,index,data):
if index < 0 or index >= self.length():
raise IndexError("Index out of range")
elif index == 0:
self.add(data)
else:
new_node = Node(data)
cur = self.head
pos = 0
while pos < index-1:
cur = cur.next
new_node.next = cur.next
cur.next = new_node
def remove(self,item):
"""删除指定元素"""
cur = self.head
pre = None
while cur is not None:
if cur.data == item:
if not pre:
self.head = cur.next
else:
pre.next = cur.next
break
else:
pre = cur
cur = cur.next
def display(self):
cur = self.head
while cur is not None:
print(cur.data)
cur = cur.next判断链表是否有环及入口索引
方法一:哈希表存储遍历结果
【源代码】:
def existLoop_hash(head):
"""哈希表判断链表是否有环"""
visited = set()
while head is not None:
if head in visited:
return True
visited.add(head)
head = head.next
return False
def findLoopBeginIndex_hash(head):
"""哈希表寻找入口节点"""
visited = {}
index = 0
while head is not None:
if head in visited:
return visited[head]
visited[head] = index
index = index + 1
head = head.next
return -1【测试代码】:
def test_hash_method():
print("===== 测试哈希法 =====")
# 测试用例1:无环链表
link1 = LinkList()
link1.append(1)
link1.append(2)
link1.append(3)
print("链表1(无环):")
print("existLoop_hash:", existLoop_hash(link1.head)) # False
print("findLoopBeginNode_hash:", findLoopBeginIndex_hash(link1.head))
print()
# 测试用例2:单节点自环
link2 = LinkList()
node = Node(1)
link2.head = node
node.next = node # 自环
print("链表2(单节点自环):")
print("existLoop_hash:", existLoop_hash(link2.head)) # True
print("findLoopBeginNode_hash:", findLoopBeginIndex_hash(link2.head))
print()
# 测试用例3:多节点有环(环入口在中间)
link3 = LinkList()
node1 = Node(1)
node2 = Node(2)
node3 = Node(3)
node4 = Node(4)
link3.head = node1
node1.next = node2
node2.next = node3
node3.next = node4
node4.next = node2 # 环入口是节点2
print("链表3(多节点有环,入口在中间):")
print("existLoop_hash:", existLoop_hash(link3.head)) # True
print("findLoopBeginNode_hash:", findLoopBeginIndex_hash(link3.head))
print()
# 测试用例4:多节点有环(环入口在头部)
link4 = LinkList()
node1 = Node(1)
node2 = Node(2)
node3 = Node(3)
link4.head = node1
node1.next = node2
node2.next = node3
node3.next = node1 # 环入口是节点1
print("链表4(多节点有环,入口在头部):")
print("existLoop_hash:", existLoop_hash(link4.head)) # True
print("findLoopBeginNode_hash:", findLoopBeginIndex_hash(link4.head))
print()
# 测试用例5:无环空链表
link5 = LinkList()
print("链表5(空链表):")
print("existLoop_hash:", existLoop_hash(link5.head)) # False
print("findLoopBeginNode_hash:", findLoopBeginIndex_hash(link5.head))
print()
test_hash_method()【测试结果】:
===== 测试哈希法 =====
链表1(无环):
existLoop_hash: False
findLoopBeginNode_hash: -1
链表2(单节点自环):
existLoop_hash: True
findLoopBeginNode_hash: 0
链表3(多节点有环,入口在中间):
existLoop_hash: True
findLoopBeginNode_hash: 1
链表4(多节点有环,入口在头部):
existLoop_hash: True
findLoopBeginNode_hash: 0
链表5(空链表):
existLoop_hash: False
findLoopBeginNode_hash: -1
【时间复杂度分析】:
本来试图使用数学归纳法来证明,但是这个函数不是递归实现的,并且对于这个迭代方式,写数学归纳法会比较麻烦,不如直接分析来的快。
数学归纳法
(1) 定义命题
设命题 P(k) 为:
“对于链表的第 k 个节点,函数在访问它时的操作时间为 O(1),且总时间不超过 k * O(1)。”
(2) 基例
k=1(头节点):执行
head in visited(O(1))和visited.add(head)(O(1))。总时间
T(1) = O(1),命题成立。
(3) 归纳假设
假设 P(k) 成立,即前 k 个节点的处理时间为 O(k)。
(4) 归纳步骤
第
k+1个节点:执行
head in visited(O(1))。若未访问过,执行
visited.add(head)(O(1))。总时间
T(k+1) = T(k) + O(1) = O(k) + O(1) = O(k+1)。
命题
P(k+1)成立。
(5)结论
由数学归纳法,对所有 n 个节点,时间复杂度为 O(n)。
(这个是ai生成的,递归函数的证明我还是能写一点的,这个确实不会,放在这提醒自己格式)
直接分析--existLoop_hash
初始化空集合操作执行次数为1
单次循环的时间:
检查节点是否访问执行次数为1
记录已访问节点执行次数为1
移动到下一节点执行次数为1
循环次数:
无环情况:遍历
n个节点后退出,循环次数为n有环情况:若环长度为
k,仍需遍历n个节点(遍历n-k次到环入口,再遍历k次经过一个环)无论有无环,循环次数均为
n
总时间复杂度:
nxO(1)=O(n)
直接分析--findLoopBeginIndex_hash
初始空集合、索引操作执行次数为1
单次循环时间:
检查节点是否访问执行次数为1
记录已访问节点执行次数为1
更新索引执行次数为1
移动到下一节点执行次数为1
循环次数同上,为
n总时间复杂度:
nxO(1)=O(n)
方法二:快慢指针法
【原理分析】:
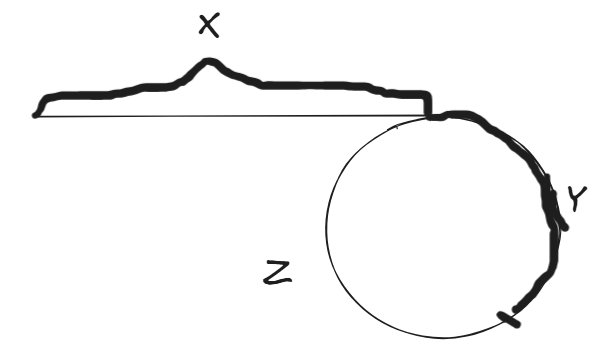
现在在链表的头节点放置两个指针,慢指针以每次1个节点的速度前进,快指针以每次2个节点的速度前进,假设头节点到入口节点的距离为x,快慢指针在环内相遇的位置到下一个入口节点需要经过z个节点,该位置距离上次经过的入口节点y个节点。
在相遇时
对于慢指针,走过的距离L1 = x + y
对于快指针,走过的距离L2 = x + y + k*(y+z)
在相同的时间内,L2 = 2*L1 ,即x = (k-1)*y + z
当k = 1时,x = z,此时在头节点和相遇节点分别放置一个指针,移动速度为1,当两个指针相遇的节点即为入口节点
【问题解析】:
“为什么慢指针没有走完一圈?”
——因为快指针速度是慢指针的两倍,示意图如下: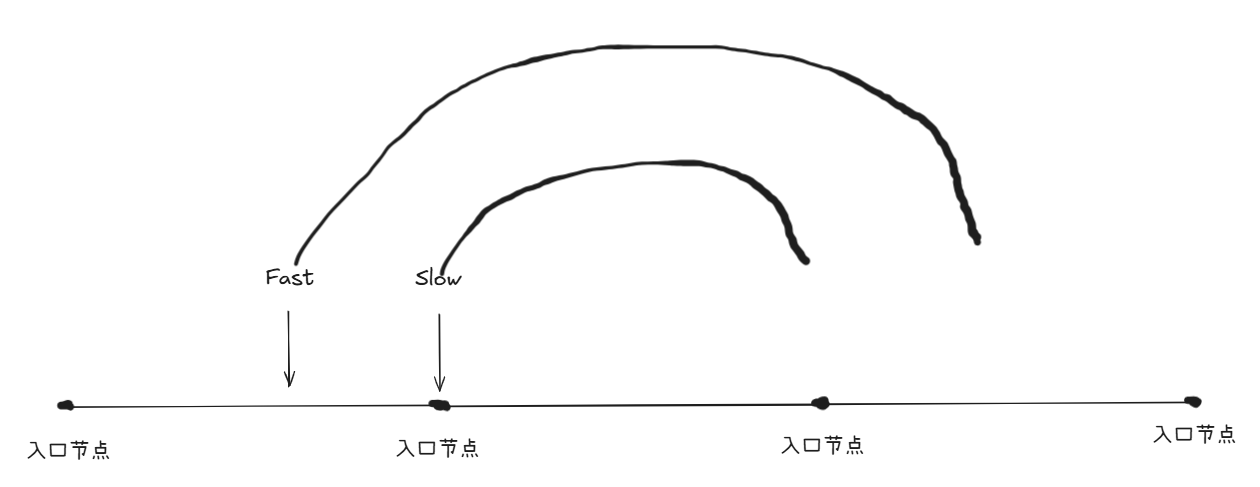
慢指针在走完一圈前就会被追到
“为什么设置快指针速度为2”
——因为快指针的速度只能设置为质数,但是速度要小于环的长度,不然会在环的部分节点循环,所以最好用的是2
【源代码】:
def existLoop(head):
if head is None:
return False
if head.next == head:
return True
slow = head
fast = head
while fast is not None and fast.next is not None:
slow = slow.next
fast = fast.next.next
if slow == fast:
return True
return False
def findLoopBeginNode(head):
if head is None or head.next is None:
return -1
if head.next == head:
return 0
slow = head
fast = head
index = 0
while fast is not None and fast.next is not None:
slow = slow.next
fast = fast.next.next
if slow == fast:
break
# 如果无环则退出
if fast is None or fast.next is None:
return -1
newNode = head
while newNode != slow:
index += 1
newNode = newNode.next
slow = slow.next
return index【测试代码】:
def test_linked_list_cycle():
class SingleNode:
def __init__(self, item):
self.item = item
self.next = None
class LinkList:
def __init__(self):
self._head = None
def append(self, item):
if not self._head:
self._head = SingleNode(item)
else:
current = self._head
while current.next:
current = current.next
current.next = SingleNode(item)
# 测试用例1:无环链表
print("=== 测试1:无环链表 ===")
link1 = LinkList()
link1.append(1)
link1.append(2)
link1.append(3)
print("链表元素:1 -> 2 -> 3")
print("existLoop 结果:", existLoop(link1._head)) # 应返回 False
print("findLoopBeginNode 结果:", findLoopBeginNode(link1._head)) # 应返回 -1
print()
# 测试用例2:单节点自环
print("=== 测试2:单节点自环 ===")
link2 = LinkList()
node = SingleNode(1)
link2._head = node
node.next = node # 自环
print("链表元素:1 -> 1 (自环)")
print("existLoop 结果:", existLoop(link2._head)) # 应返回 True
print("findLoopBeginNode 结果:", findLoopBeginNode(link2._head)) # 应返回 0
print()
# 测试用例3:多节点有环(环入口在中间)
print("=== 测试3:多节点有环(环入口在中间) ===")
link3 = LinkList()
node1 = SingleNode(1)
node2 = SingleNode(2)
node3 = SingleNode(3)
node4 = SingleNode(4)
link3._head = node1
node1.next = node2
node2.next = node3
node3.next = node4
node4.next = node2 # 环入口是节点2
print("链表元素:1 -> 2 -> 3 -> 4 -> 2 (环)")
print("existLoop 结果:", existLoop(link3._head)) # 应返回 True
print("findLoopBeginNode 结果:", findLoopBeginNode(link3._head)) # 应返回 1
print()
# 测试用例4:多节点有环(环入口在头部)
print("=== 测试4:多节点有环(环入口在头部) ===")
link4 = LinkList()
node1 = SingleNode(1)
node2 = SingleNode(2)
node3 = SingleNode(3)
link4._head = node1
node1.next = node2
node2.next = node3
node3.next = node1 # 环入口是节点1
print("链表元素:1 -> 2 -> 3 -> 1 (环)")
print("existLoop 结果:", existLoop(link4._head)) # 应返回 True
print("findLoopBeginNode 结果:", findLoopBeginNode(link4._head)) # 应返回 0
print()
# 测试用例5:无环空链表
print("=== 测试5:无环空链表 ===")
link5 = LinkList()
print("链表元素:空")
print("existLoop 结果:", existLoop(link5._head)) # 应返回 False
print("findLoopBeginNode 结果:", findLoopBeginNode(link5._head)) # 应返回 -1
print()
# 运行测试
test_linked_list_cycle()【测试结果】:
=== 测试1:无环链表 ===
链表元素:1 -> 2 -> 3
existLoop 结果: False
findLoopBeginNode 结果: -1
=== 测试2:单节点自环 ===
链表元素:1 -> 1 (自环)
existLoop 结果: True
findLoopBeginNode 结果: 0
=== 测试3:多节点有环(环入口在中间) ===
链表元素:1 -> 2 -> 3 -> 4 -> 2 (环)
existLoop 结果: True
findLoopBeginNode 结果: 1
=== 测试4:多节点有环(环入口在头部) ===
链表元素:1 -> 2 -> 3 -> 1 (环)
existLoop 结果: True
findLoopBeginNode 结果: 0
=== 测试5:无环空链表 ===
链表元素:空
existLoop 结果: False
findLoopBeginNode 结果: -1
【时间复杂度分析】:
existLoop函数时间复杂度分析:
两个判断语句执行次数为1
初始化快慢指针执行次数为1
单次循环执行时间:
移动快慢指针执行次数为1
判断快慢指针是否相遇执行次数为1
循环次数:
无环:遍历整个链表,次数为n
有环:最坏情况下,尾节点形成自环,快慢指针在尾节点相遇,次数为n
总时间时间复杂度:
nxO(1)=O(n)
findLoopBeginNode函数:
两个判断语句执行次数为1
初始化快慢指针执行次数为1
初始化索引执行次数为1
第一阶段:检测环
最坏情况:快指针遍历整个链表,执行
n/2次,O(n)最好情况:快慢指针相遇时,最多遍历
n次,O(n)
第二节点:寻找入口
最多需要
x步,x≤n,O(n)
总时间时间复杂度:
O(n)+O(n)=O(n)
排序
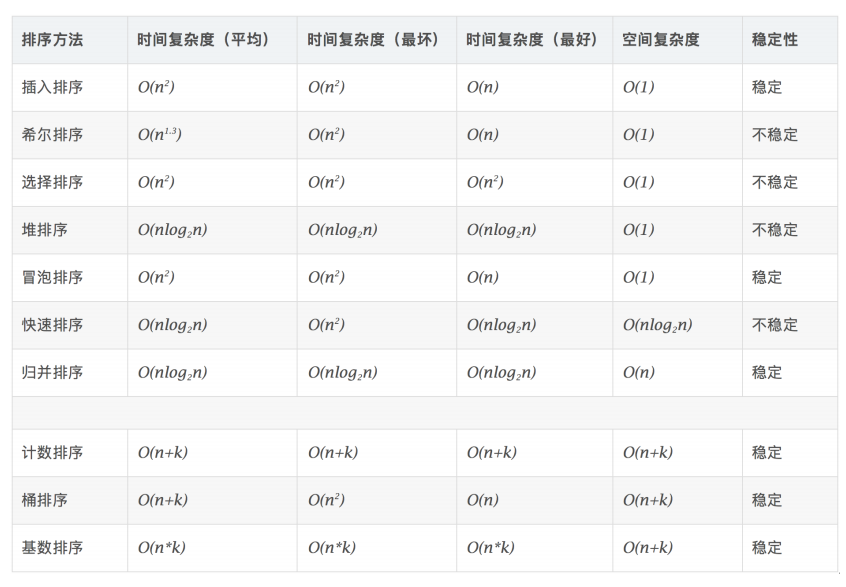
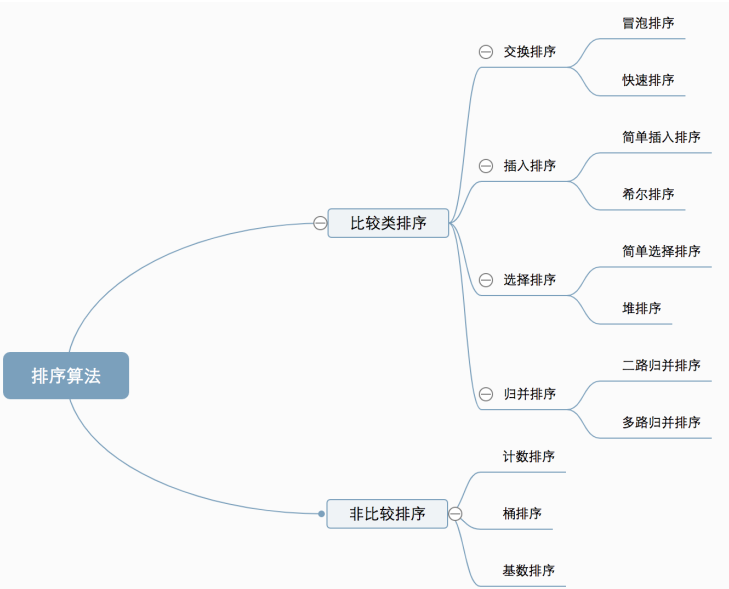
代码文件如下:
【补充】:希尔排序中间隔序列gap的选择
1.Shell原始序列公式:gap = ⌊2/n⌋,,⌊4/n⌋,...,1,…,1
简单易实现,但时间复杂度较差(最坏情况下为O(n2))
由于gap之间是二分递减,可能导致某些分组重复比较
(当序列为逆序排列的时候,该方式无法有效减小逆序对,最终仍然需依赖gap=1的插入排序)
2.Kunth序列公式: gap = (3k-1)/2 (直到gap > n/3)
时间复杂度约为O(n1.5),优于Shell原始序列
数学上更高效,但计算稍复杂
3.Sedgewick序列公式:gap = 9
x4i-9x2i+1目前已知最优的gap序列之一,时间复杂度可接近O(n1.3)
适用于大规模数据
4.Hibbard序列公式: gap = 2k
-1时间复杂度为O(n1.5)
避免Shell原始序列的重复比较问题