大模型入门(1)——“人人都能看懂的RL-PPO理论知识”
在攻读第一篇文章“GPG-A Simple and Strong Reinforcement Learning Baseline for Model Reasoning”后发现自己在Method的策略梯度(PG)公式没看懂,所以先看看这一篇博客入门PPO和LLM的相关知识。
一、参考教程
Sutton的《强化学习导论》:https://rl.qiwihui.com/zh-cn/latest/notation.html
(主要要了解价值函数,了解什么是value-based,policy-based,actor-based)
蘑菇书EasyRL:https://datawhalechina.github.io/easy-rl/#/chapter2/chapter2
二、主要内容
介绍policy-based下的优化目标
介绍价值函数的相关定义
引入actor-critic,讨论在policy-based的优化目标中,对“价值”相关的部分如何做优化
基于actor-critic的知识介绍PPO
2.1 策略(Policy)
策略分为两种:确定性策略和随机性策略。一般用θ表示策略的参数。
2.1.1 确定性策略
at = μθ(st)
智能体在看到状态st的情况下,确定地执行at
2.1.2 随机性策略
at ~ πθ(.|st)
智能体在看到状态st的情况下,其可能执行的动作服从概率分布πθ(.|st)。也就是此时智能体是以一定概率执行某个动作at
2.2 奖励(Reward)
奖励由当前状态、已经执行的行动和下一步的状态共同决定。
2.2.1 单步奖励
rt = R(st,at,st+1)
奖励和策略π无关
用于评估当前动作的好坏,指导智能体的动作选择
2.2.2 T步累积奖励
T步累积奖励等于一条运动轨迹/一个回合/一个rollout后的单步奖励的累加
(敲不了复杂数学公式的屑博客)
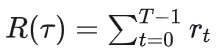
2.2.3 折扣奖励
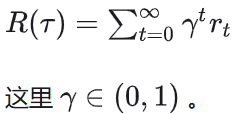
2.3 运动轨迹(trajectory)和状态转移
智能体和环境做一系列/一回合交互后得到的state、action和reward的序列,所以运动轨迹也被称为episodes或rolloutes,这里假设智能体与环境交互了T次:
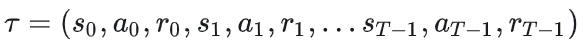
s0是初始时智能体所处的状态,它只和环境有关。假设一个环境中的状态服从分布ρ0,则有s0~ρ0(.)
当智能体在某个st下采取动作at时,它转移到某个状态st+1可以说确定的,也可以是随机的:
确定的状态转移:st+1=f(st,at),表示的含义是当智能体在某个st下采取某个动作at时,环境的状态确定性地转移到st+1
随机的状态转移:st+1~P(.|st,at)
接下来的介绍中,假设环境采用的是随机状态转移
2.4 Policy-based强化学习优化目标
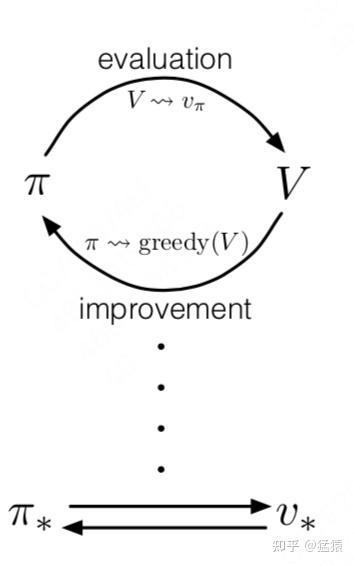
强化学习的优化过程可以总结为:
价值评估:给定一个策略π,如何准确评估当前策略的价值Vπ?
策略迭代:给定一个当前策略的价值评估Vπ,如何据此优化策略π?
整个优化过程由以上两点交替进行,最终收敛到最优策略π*和能准确评估它的价值函数Vπ*。
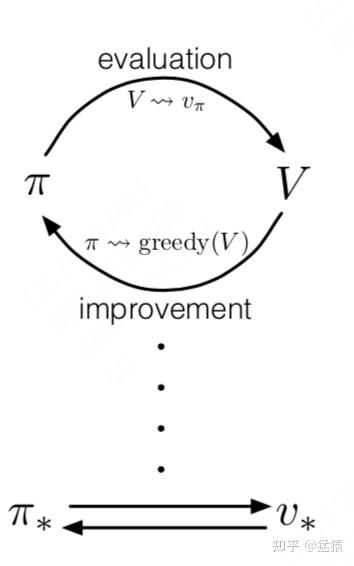
【问题】:这是否意味着强化学习过程中一定存在π和Vπ两个实体呢?例如,这是否意味着我们一定要训练两个神经网络,分别表示策略和价值评估?
答案是否定的:
只有一个价值实体Vπ,因为它的输入和状态与动作相关。这意味着只要我们知道状态空间S和动作空间A,Vπ就可以作用到这两个空间上帮助我们衡量哪个状态/动作的价值最大,进而隐式地承担起制定策略的角色。这种方式被称为value-based。
只有一个策略实体π,在对策略的价值评估中,我们可以让策略和环境交互多次,采样足够多的轨迹数据,用这些数据去对策略的价值做评估,然后再据此决定策略的迭代方向。这种方式被称为policy-based
同时有价值实体Vπ和策略实体π,然后按上面的过程进行迭代,这种方法被叫做actor-critic,其中actor表示策略,critic表示价值。
policy-based下的强化学习优化目标为:
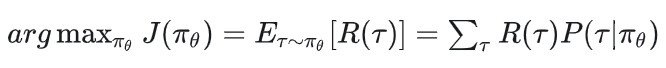
其中:

2.5 策略的梯度上升
2.5.1 基本推导
知道了总的优化目标后,计算梯度:


【注】:P(st+1|st,at)表示在时间步t时,给定当前状态st和智能体采取的动作at的条件下,下一个状态是st+1的概率。这是环境的动力学模型(或状态转移概率),它描述了环境如何响应智能体的动作。
2.5.2 总结
在基于策略的强化学习中,我们期望最大化以下优化目标:
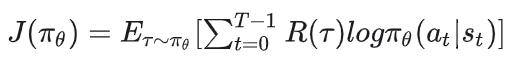
基于这个优化目标,策略πθ的梯度为:
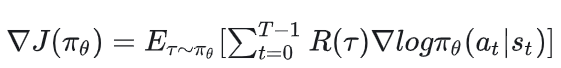
这个梯度表达式有个简单的直观理解:当R(τ)越高时,动作at贡献的梯度应该越多,这是因为此时我们认为at是一个好动作,因此我们应该提升πθ(at|st),即提升在st下执行at的概率,反之亦然。
在实践中,我们可以通过采样足够多的轨迹来估计这个期望。假设采样N条轨迹,N足够大,每条轨迹涵盖Tn步,则上述优化目标可以再次被写成:

2.6 价值函数(Value Function)
通过上面的推导,我们知道在强化学习中,策略的梯度可以表示为:
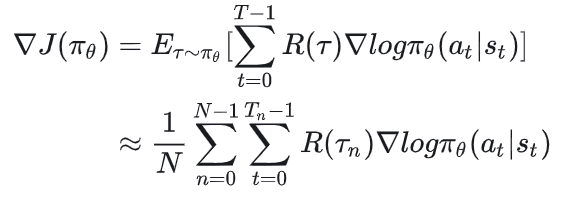
这里R(τ)表示一整条轨迹的累积奖励或者累积折扣奖励。
【问题】:R(τ)是整条轨道的奖励,而πθ(at|st)却是针对单步的。用整体轨迹的回报评估单步的价值,然后决定要提升/降低对应at的概率,可能不太合理:
一条轨迹最终的回报很高,并不能代表这条轨迹中的每一个动作都是好的
但我们又不能完全忽视轨迹的最终回报,因为我们的最终目标是让这个回合的结果是最优的
综上,在衡量单步价值时,我们最好能在【单步回报】和【轨迹整体回报】间找到一种平衡方式
使用一个ψt来替换R(τ),策略的梯度变成:
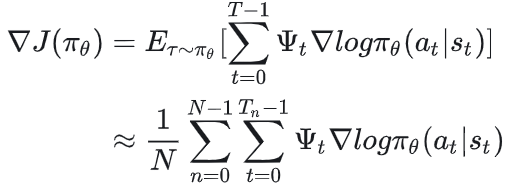
2.6.1 总述:衡量价值的不同方式
总的来说ψt可能有如下的实现方式:
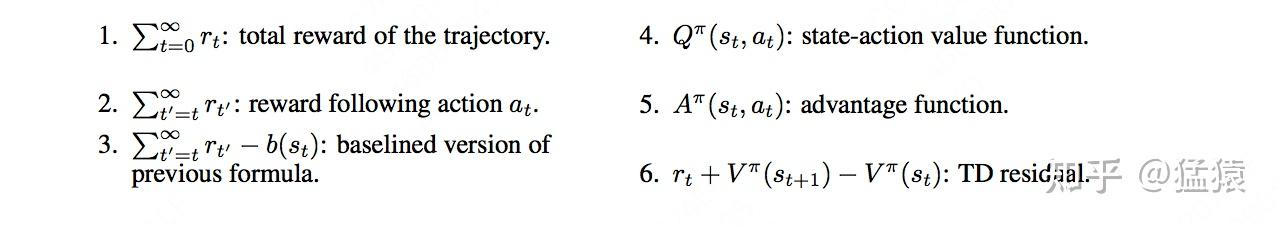
(1)整条轨迹累积奖励/累积折扣奖励
这是前文一直沿用的方法,即:
ψt=R(τ)
(2)t时刻后的累积奖励/累积折扣奖励
由于MDP(马尔可夫决策过程)的假设,t时刻前发生的事情和t时刻没有关系,t时刻后发生的事情才会收到t时刻的影响,因此令:
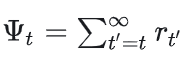
(3)引入基线

(4)动作价值函数 Qπ(st,at)
(5)优势函数 Aπ(st,at)
(6)状态价值的TD error rt+γVπ(st+1)-Vπ(st)


2.6.2 回报

2.6.3 状态价值函数(State-Value Function)
评价的是一个状态的好坏

上面是状态价值函数最原子的定义,我们把这个定义展开,以便更好理解 是如何计算的:(不全,但是明白就行)


2.6.4 动作价值函数(Action-Value Functin)
评价的是一个状态-动作对的好坏

2.6.5 动作价值函数和状态价值函数的互相转换


2.6.6 优势函数和TD error


2.7 Actor-Critic

2.7.1 Actor优化目标

2.7.2 Critic优化目标

2.7.3 Actor和Critic之间的关系


2.8 PPO
2.8.1 朴素Actor-Critic的问题

2.8.2 重要性采样


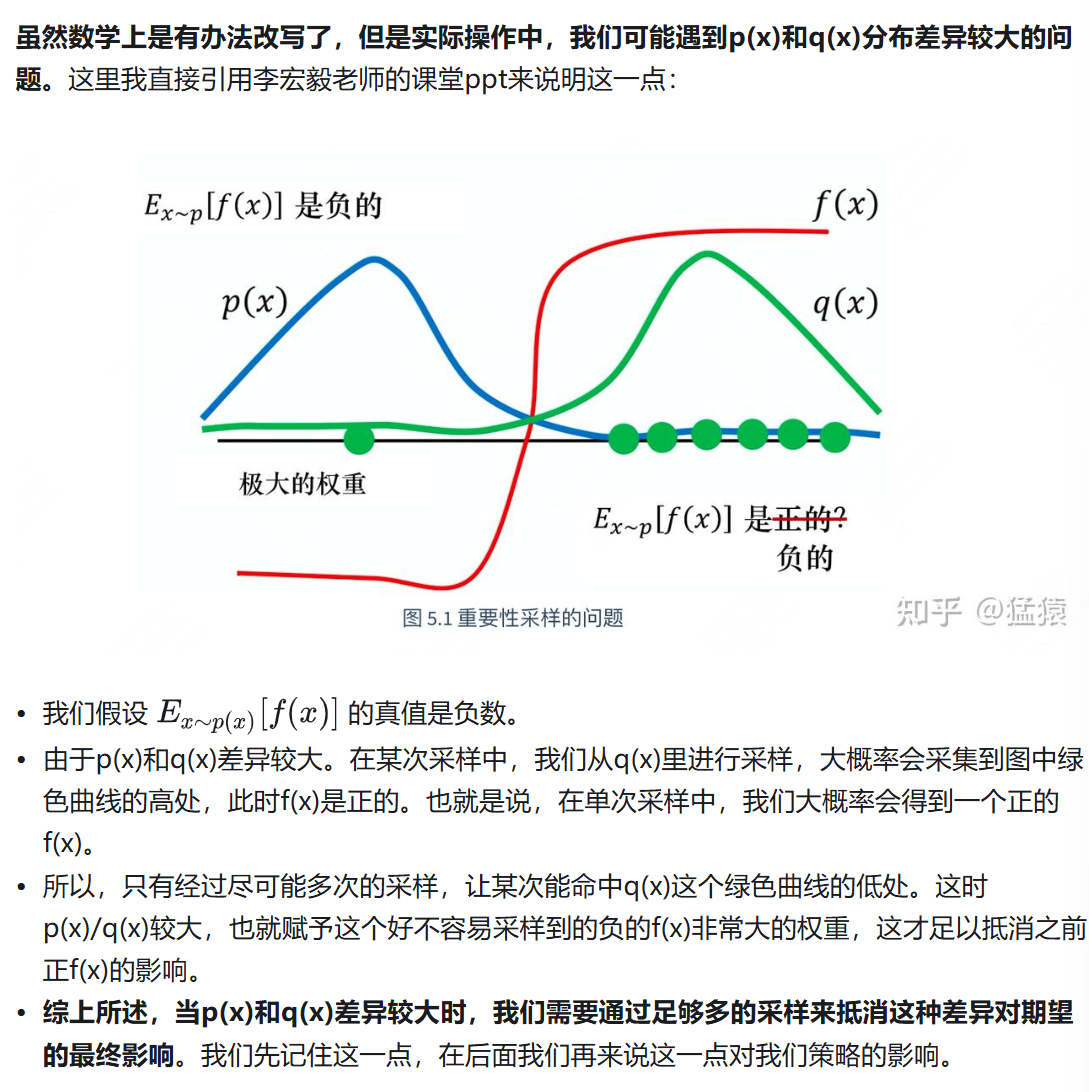

2.8.3 GAE:平衡优势函数的方差和偏差

(1)方差与偏差
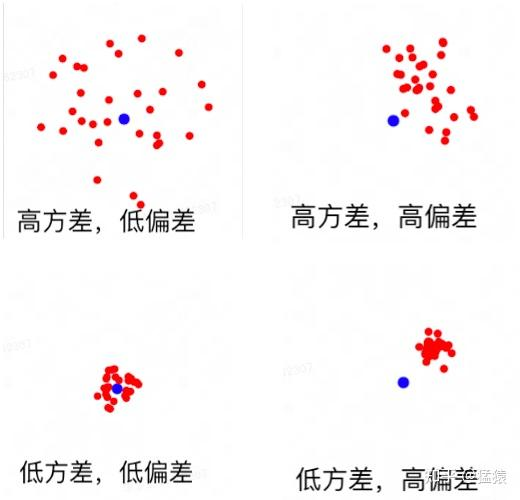



(2)GAE

2.8.4 PPO前身:TRPO
